数据结构与算法 --- 排序算法（二）

引言

上一篇数据结构与算法 --- 排序算法（一）中，学习了冒泡排序，插入排序，选择排序这三种时间复杂度为 $O(n^2)$ 的算法。实时上 $O(n^2)$ 时间复杂度是非常高的，所以一般只适合小规模数据排序，那接下来，就在看一看时间复杂度为 $O(nlog)$ 的算法：归并排序和快速排序。

分治算法思想

归并排序和快速排序的核心思想就是分治算法思想，所以先介绍一下分治算法思想：

分治算法思想简单来说就是将一个复杂的问题分解成几个较简单的子问题，再递归地解决这些子问题。通常遵循以下三个步骤:

分解：将问题分解成几个较小的子问题，这些子问题必须是相同类型的问题，且解决这些子问题必须可以解决原问题。
解决：递归地解决各个子问题，如果子问题足够小可以直接解决则解决，否则继续分解。
合并：将子问题的解合并为原问题的解。

归并排序

归并排序（Merge Sort）是一种基于分治思想的排序算法。它的基本思路是将待排序的数组分成两个子序列，然后对每个子序列进行递归排序，最后将排好序的两个子序列合并成一个有序序列。

算法图解

来看一下归并排序的执行过程如下图：

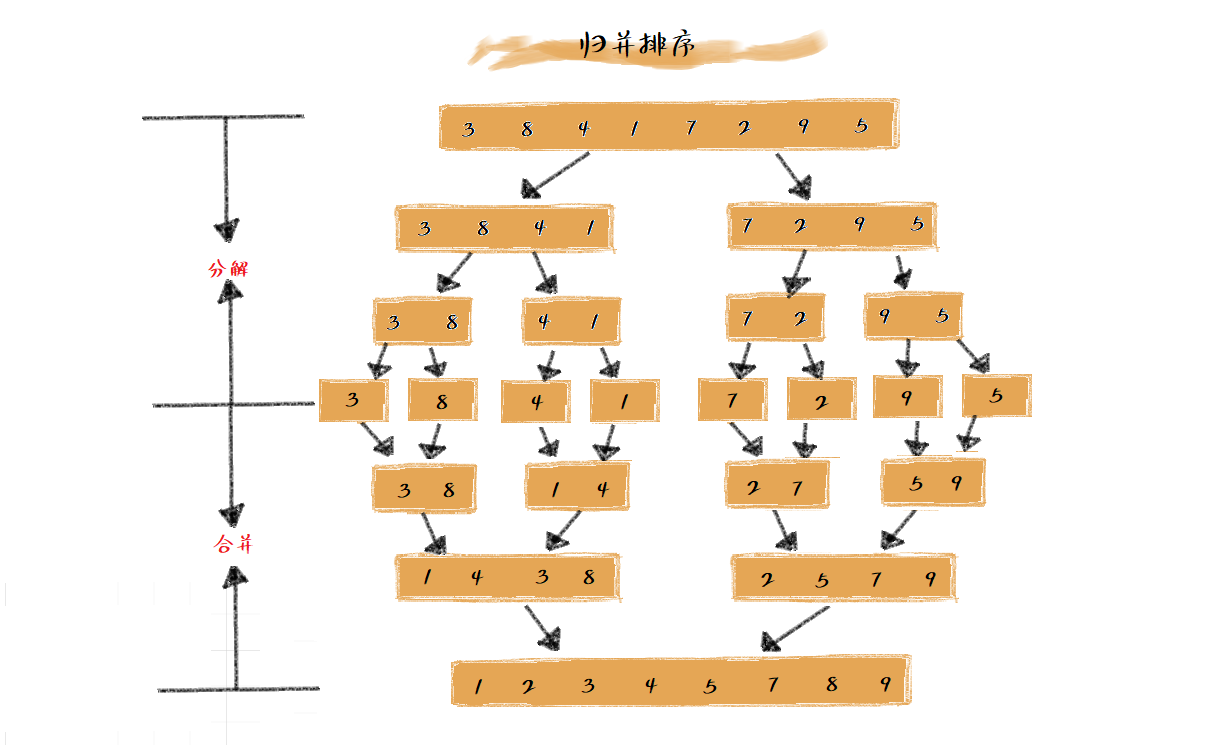
接下来考虑如何使用C#代码实现一个归并排序算法？

一般归并排序就是通过递归实现的，那么在数据结构与算法 --- 递归（一）中总结了递归代码的编写技巧：写递推公式，寻找终止条件，最后将递推公式翻译为代码。

那么看一下归并排序的递归代码的递推公式为：

merge\_sort(p,r)=merge(merge(p,q),merge(q+1,r)), \quad (p<q<r)

其终止条件为: $p\ge r$ 。

公式中 $merge\_sort(p,r)$ 表示对下标从 $p$ 到 $r$ 的数组数据进行归并排序，然后将这个问题拆分成了两个子问题： $merge(p,q)$ 和 $merge(q+1,r)$ ，其中下标 $q$ 表示 $p$ 到 $r$ 的中间位置，也就是 $\frac{p+r}{2}$ ，当这两个子数组排好序之后，再将这两个有序子数组合并（ $merge()$ ），就完成了该数组的排序。

这里还需要着重讲解一下两个有序子数组的合并，实际上一般在这里合并方法使用的是双指针法，双指针法是合并两个有序数组最高效的算法，其时间复杂度为 $O(m+n)$ ，其中 m 和 n 分别是两个数组的长度。具体实现步骤如下：

定义两个指针 i 和 j，分别指向两个有序数组的起始位置。
定义一个空数组 temp，用于存储合并后的有序数组。
比较两个指针所指的元素大小，将较小的元素加入 temp 数组中，并将对应的指针向后移动一位。
重复步骤 3，直到其中一个指针超出了数组的范围。
将另一个数组中剩余的元素加入 temp 数组中。
最后将temp中的元素拷贝回arr中,完成排序。

综上，用C#代码实现一个归并算法如下：

csharp
public static void MergeSort(int[] arr, int left, int right)
{
    if (left < right)
    {
        int mid = (left + right) / 2;
        //将待排序的数组分成两个子序列进行递归排序
        MergeSort(arr, left, mid);
        
        MergeSort(arr, mid + 1, right);
        //合并
        Merge(arr, left, mid, right);
    }
}

public static void Merge(int[] arr, int left, int mid, int right)
{
    //双指针法合并数据到temp数组
    int i = left, j = mid + 1, k = 0;
    
    int[] temp = new int[right - left + 1];
    
    while (i <= mid && j <= right)
    {
        if (arr[i] <= arr[j])
        {
            temp[k] = arr[i];
            i++;
        }
        else
        {
            temp[k] = arr[j];
            j++;
        }
        k++;
    }
    //当一边遍历完成后,将另一边剩余元素直接放入temp。
    while (i <= mid)
    {
        temp[k] = arr[i];
        i++;
        k++;
    }
    while (j <= right)
    {
        temp[k] = arr[j];
        j++;
        k++;
    }
    for (int p = 0; p < k; p++)
    {
        arr[left + p] = temp[p];
    }
}

算法分析

稳定性：

归并排序是否稳定关键要看 Merge() 方法这部分逻辑。

在合并过程中，如果前半部分（图解左侧）和后半部分（图解右侧）之间有相同元素，先把前半部分中相同的值放入临时数组temp，再把后半部分中的相同的值放入临时数组temp，那么就能保证值相同的元素在合并前后的先后顺序不变，因此，归并排序是稳定排序算法。

时间复杂度：

归并排序的时间复杂度可以通过递归树和递推式来分析，具体分为以下几个步骤：

分解：将待排序的数组逐步分解成更小的子数组，直到每个子数组只有一个元素。
合并：将相邻的子数组两两合并，形成更大的有序子数组。
递归：对合并后的有序子数组重复上述步骤，直到最终得到完全有序的数组。

现在我们来分析归并排序的时间复杂度：

分解步骤：在每一次分解过程中，数组被均分为两部分，所以分解的时间复杂度是 $O(logn)$ ，其中n是待排序数组的长度。
合并步骤：合并操作需要比较每个子数组中的元素，并将它们按照顺序放入新的临时数组中。在最坏情况下，每个子数组的长度为 $\frac{n}{2}$ ，所以合并的时间复杂度是 $O(n)$ 。而在每一层的递归中，总共有 $n$ 个元素需要进行合并操作，所以合并的时间复杂度也是 $O(n)$ 。
递归步骤：归并排序通过递归调用对子数组进行排序，每次将数组的长度减半。因此，总共进行 $logn$ 次递归操作。

综上所述，归并排序的时间复杂度可以表示为：

T(n) = O(logn) \times O(n) = O(nlogn)

所以，归并排序的时间复杂度是O(nlogn)。无论输入数组的初始状态如何，归并排序的时间复杂度都保持不变。

内存消耗： 很明显，归并排序使用了额外的内存空间，所以它不是原地排序算法。

我们不能像分析时间复杂度那样分析空间复杂度，因为空间复杂度是一个峰值，而时间复杂度是一个累加值，递归代码的空间消耗并不能像时间消耗那样累加，空间复杂度表示在程序运行过程中的最大消耗，而不是累加的内存消耗。

尽管每次合并操作都需要申请额外的临时数组temp，但在函数完成之后，临时数组temp所占的内存就被释放了。

在任意时刻，只会有一个函数在执行，也就只会有一个临时数组temp在使用，占用的临时空间内存最大也不会超过 n 个数据的大小，对应的空间复杂度也就是 $O(n)$ 。

除此之外，在归并排序的过程中，递归调用栈的空间复杂度取决于递归深度。对于一个长度为n的数组进行归并排序，递归深度为log₂n。每一层递归都需要保存一些临时变量，如左右指针、中间指针等，这些变量的空间复杂度为 $O(1)$ 。因此，递归调用栈的空间复杂度为 $O(log₂n)$ 。

综上所述，归并排序的空间复杂度为 $O(logn + n)$ 。可以省略低阶部分，那就是 $O(n)$ 。

参考

[1] 数据结构与算法之美 / 王争著. --北京：人民邮电出版社，2021.6

目录

引言

分治算法思想

归并排序

算法图解

算法分析