目录
意义
算法复杂度分析的意义在于评估算法的执行效率,找出最优解决方案,是优化算法和改进程序性能的基础。通过对算法的时间复杂度和空间复杂度进行分析,可以帮助我们预估该算法运行所需的资源,从而提高程序的性能。
大O复杂度表示法
例1
有如下代码
csharp1 public int Calculate(int n)
2 {
3 int sum = 0;
4 for (int i = 0; i < n; i++)
5 {
6 sum += i;
7 }
8 return sum;
9 }
上述代码段中,假设每条语句执行的时间一样,为1个单位,记为。那么在上述代码片段中:
-
第3、8行执行分别需要1
-
第4、5、6、7行代码循环执行了次,那么就需要个
-
总的执行时间为个。
我们借助在线函数绘图工具画出该函数的曲线如下:
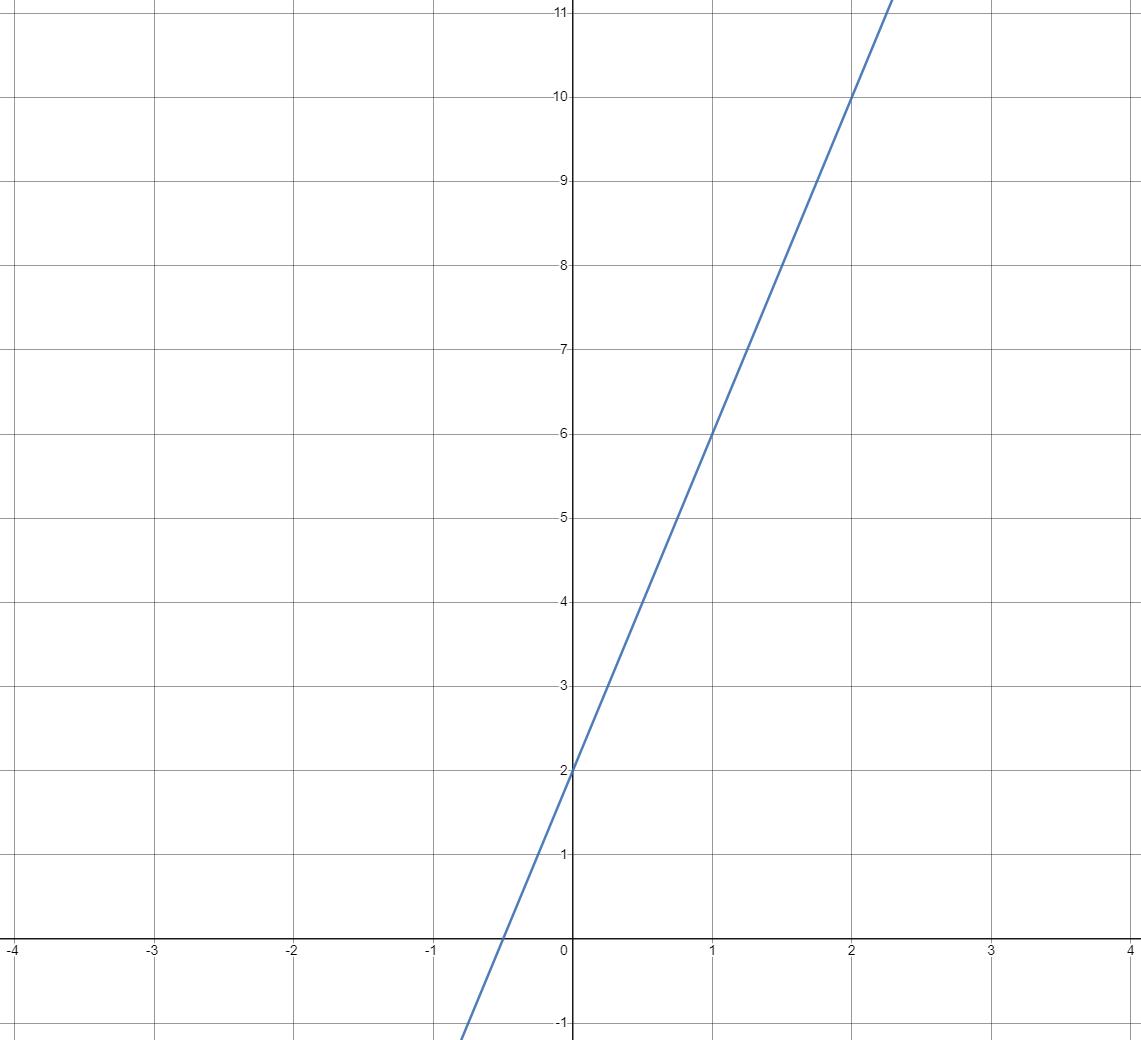
我们可以看出一个规律:执行时间一定为正数,所以代码执行的总时间(()X)是和语句的执行次数()成正比的。
例2
csharp1 public int Calculate(int n)
2 {
3 int sum = 0;
4 for (int i = 0; i < n; i++)
5 {
6 for (int j = 0; j < n; j++)
7 {
8 sum += i;
9 }
10 }
11 return sum;
12 }
同上,假设每条语句执行的时间一样,为1个单位,记为。那么在上述代码片段中:
-
第3、11行分别需要
-
第4、5、10行分别循环执行了次,即执行需个
-
第6,7,8,9分别执行了次,即执行需个
-
总的执行时间为个
画出该函数的曲线如下:
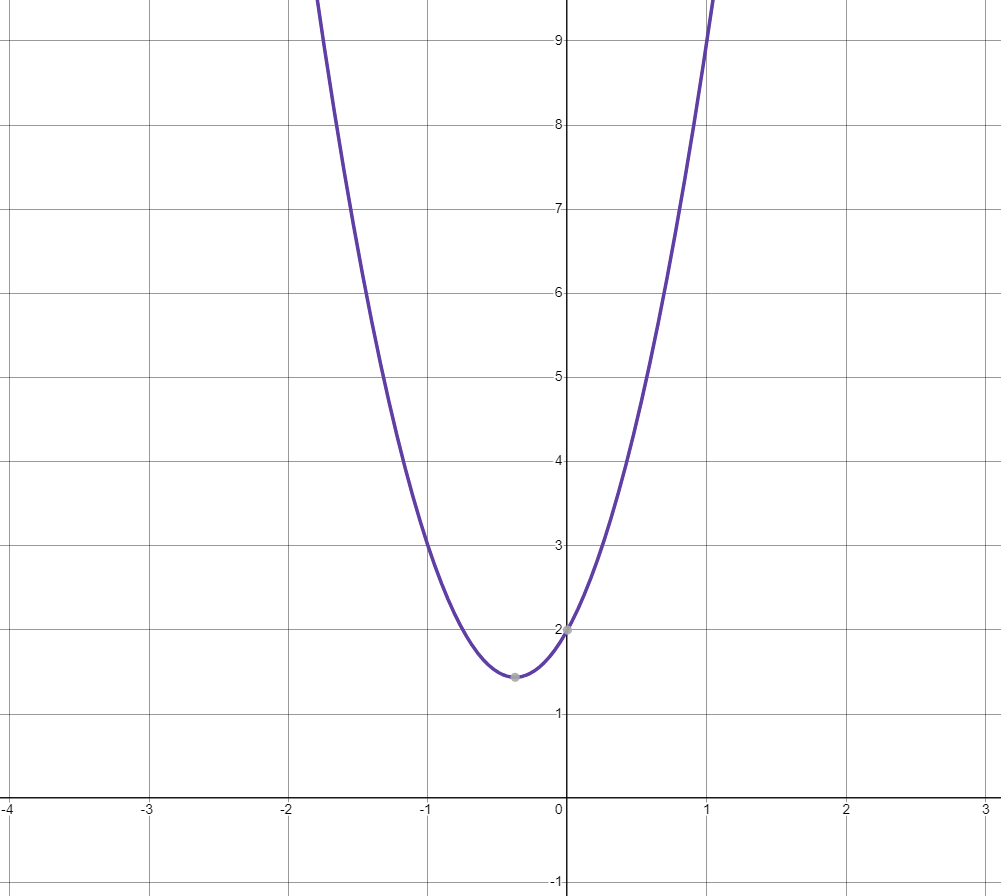
由上边两段推导代码执行时间的过程,可以得到一个重要规律:一段代码的执行时间与每一条语句的总执行次数(累加数)成正比,可以把这个规律总结为一个公式,如下:
其中,表示代码执行的总时间,表示数据规模,表示每条语句执行次数的累加和,这个值与有关,因此用这样一个表达式来表示,公式中的符号,表示代码的执行时间与成正比。
实际上,大时间复杂度并不具体表示代码真正执行的时间,而是表示代码执行时间随着数据规模增大的变化趋势,因此,也称为渐近时间复杂度(asymptomatic time complexity),简称时间复杂度。
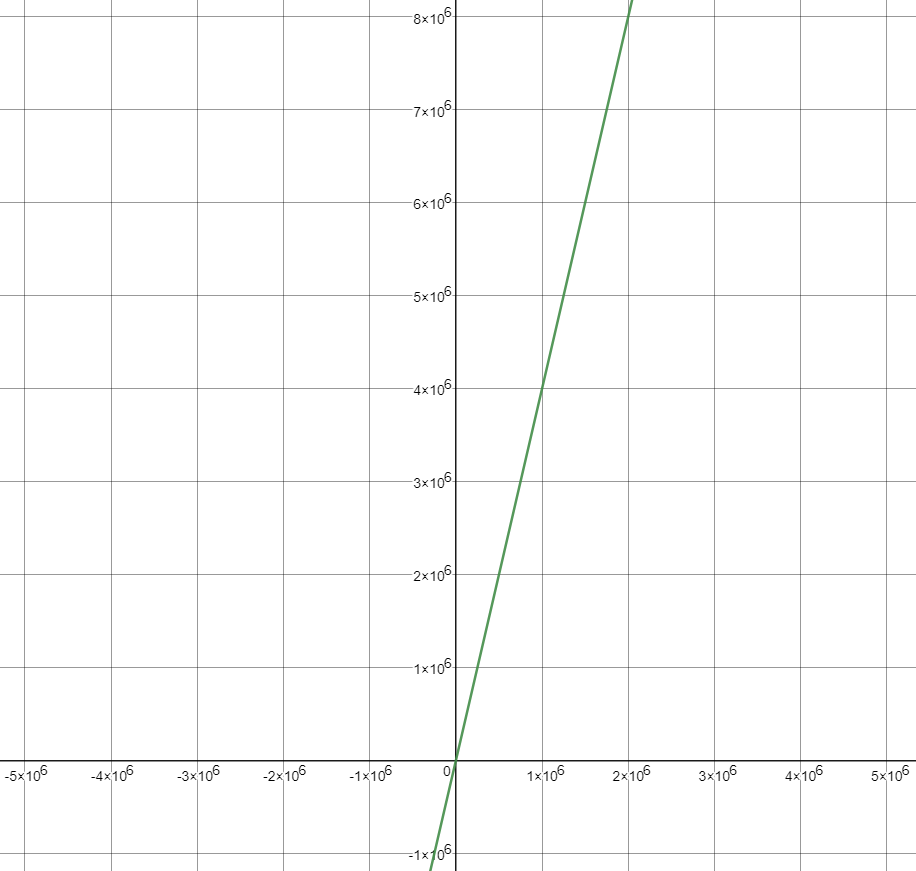
当很大时,100000,1000000级别时,公式中的低阶,常量,系数3部分并不左右增长趋势,例如下面的曲线:
曲线:
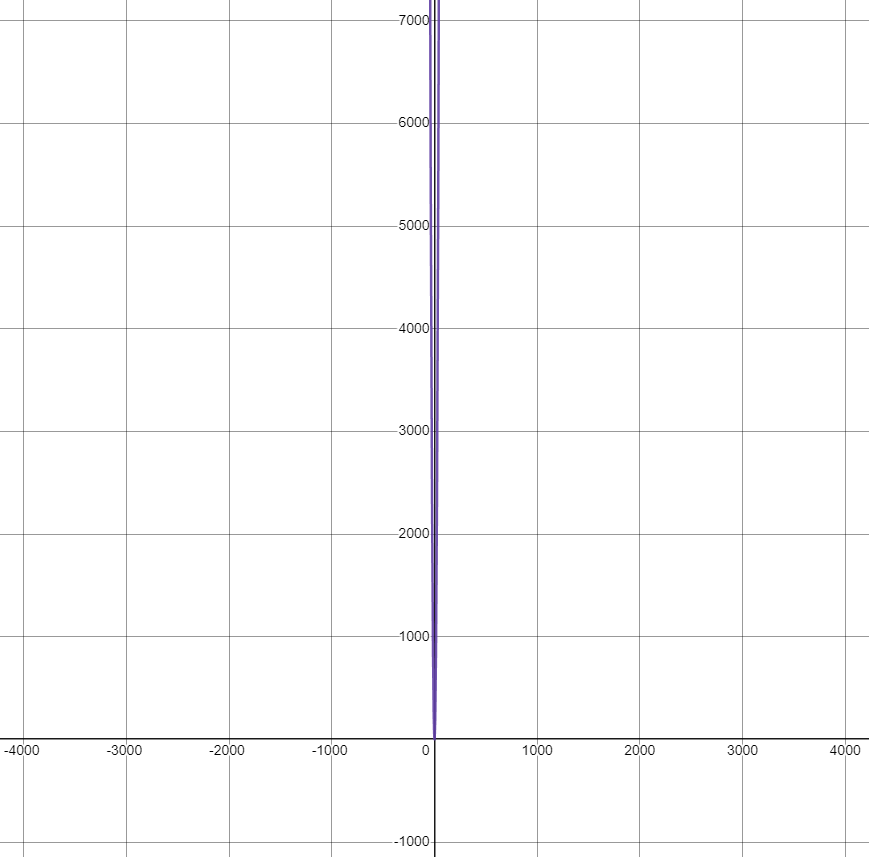
曲线,该曲线即使只到十位数的数量级,曲线就已经趋向于笔直的竖线:
所以低阶,常量,系数3部分可以忽略。我们只需要记录一个最大量级。如果用大表示法表示上面的两个复杂的则是这样:
时间复杂度的分析方法
大O复杂度表示方法只表示一种变化趋势,我们通常会忽略公式中的常量,低阶和系数,只记录最大量级,因此,我们在分析一段代码时间复杂度的时候,我们也只需要关注循环执行次数最多的那段代码。
加法法则
加法法则:代码的总复杂度等于量级最大的那段代码的复杂度。
有如下代码片段,分析一下它的时间复杂度:
csharppublic int Calculate(int n)
{
//第一段
int sum1 = 0;
for (int i = 0; i < 100; i++)
{
sum1 += i;
}
//第二段
int sum2 = 0;
for (int i = 0; i < n; i++)
{
sum2 += i;
}
//第三段
int sum3 = 0;
for (int i = 0; i < n; i++)
{
for (int j = 0; j < n; j++)
{
sum3 += i;
}
}
//第四段
return sum1+ sum2+ sum3;
}
分析结果:
-
第一段,执行时间固定为常数,复杂度记为。
-
第二段,复杂度为。
-
第三段,复杂度为。
-
第四段,只执行一次,复杂度记为。
提示
为什么第一段复杂度为常数?
注意大O复杂度的概念,时间复杂度表示的是代码执行时间随数据规模()的增长趋势,第一段代码中,无论如何变化,它始终执行100次。在曲线图上画出来就是一条平行于X轴的直线,并不会体现出增长趋势,
加法法则定义代码的总复杂度等于量级最大的那段代码的复杂度,用公式表达则是
如果有
那么
所以结论就是Calculate方法的时间复杂度为。
乘法法则
乘法法则:嵌套代码的复杂度等于嵌套内外代码复杂度的乘积。
有如下代码片段,计算CalculateA方法的时间复杂度:
csharppublic int CalculateA(int n)
{
int sum = 0;
for (int i = 1; i <= n; i++)
{
sum += CalculateB(n);
}
return sum;
}
public int CalculateB(int n)
{
int sum = 0;
for (int i = 1; i <= n; i++)
{
sum += i;
}
return sum;
}
分析结果:
-
CalculateA方法的时间复杂度为。 -
CalculateB方法的时间复杂度为。
乘法法则定义嵌套代码的复杂度等于嵌套内外代码复杂度的乘积,用公式表达则是
如果有
那么
所以结论就是CalculateA的时间复杂度为=
常见的时间复杂度量级
常量级
只要代码的执行时间不随数据规模变化,代码就是常量级时间复杂度,统一记作。
注意
是常量级时间复杂度的一种表示方法,并不意味着只执行了一行代码。
对数阶
对数阶时间复杂度非常常见,但它是最难分析的时间复杂度之一。
有如下代码段:
csharppublic int Calculate(int n)
{
int i = 1;
while (i <= n)
{
i *= 2;
}
return i;
}
如果想要分析该方法的时间复杂度,那就需要看执行次数最多的语句,一共执行多少次?
由上述代码中可以看出,变量i从1开始取值,每循环一次就乘以2,当i值大于n时,循环结束。写成公式则是这样:
我们简化一下就是这样:
所以得出解为:x的值为以2为底,n的对数
所以上文Calculate方法的时间复杂度为
那如果我们把上述代码段中的i *= 2 修改为i *= 3,得到的时间复杂度就变成了
那为什么标题中的表示的时间复杂不体现对数的底数呢?
因为根据对数的换底公式,
因此
其中是一个常量,采用大O复杂度表示法的时候,忽略系数,即
因此,
所以对于对数阶时间复杂度,忽略对数的底数,统一表示为。
多数据规模
这是一种特殊情况,时间复杂度由多个数据规模来决定。
有如下代码:
csharppublic int CalculateA(int m, int n)
{
int sum = 0;
for (int i = 1; i <= m; i++)
{
sum += i;
}
for (int i = 1; i <= n; i++)
{
sum += i;
}
return sum;
}
public int CalculateB(int m, int n)
{
int sum = 0;
for (int i = 1; i <= m; i++)
{
for (int j = 1; j <= n; j++)
{
sum += i;
}
}
return sum;
}
上述代码中,m,n表示两个无关的数据规模,最终代码的复杂度跟这两者都有关系,对于这两者无法事先评估谁的量级更大,所以在表达时间复杂度时都不可以省略,因此,上述代码中
- CalculateA符合加法法则,m,n不可省略,则得到的时间复杂度为
- CalculateB符合乘法法则,m,n不可省略,则得到的时间复杂度为
空间复杂度
时间复杂度全称渐近时间复杂度,表示算法的执行时间于数据规模之间的增长关系,类比一下就能得到空间复杂度定义:
空间复杂度全称渐近空间复杂度,表示为算法的存储空间与数据规模之间的增长关系。
其分析规则与时间复杂度一致,类比学习即可。常见的空间复杂度有,,,, 等。其中,对数阶复杂度常见于递归代码。
参考资料
[1] 数据结构与算法之美 / 王争 著. --北京:人民邮电出版社,2021.6
[2] 大话数据结构 / 程杰 著. --北京:清华大学出版社,2011.6
本文作者:Peter.Pan
本文链接:
版权声明:本博客所有文章除特别声明外,均采用 BY-NC-SA 许可协议。转载请注明出处!
